素数2357素数ってなぁに？
素数とは、1と、その数自身でしか割り切れない整数のこと。
たとえば、3は1で割り切れて3で割り切れますが、そのほかに割り切れる数字がありません。
7もそうだし、11も13も同様ですから、これらは素数と言えます。
2357という数字も、1で割り切れ、それ以外に割り切れる数字は2357しかありません。
したがって2357は素数です。
このように、1と、その数自身でなければ割り切れない整数を素数と言います。
2018年1月現在わかっている最大の素数は、2324万9425桁にもなる大きな数字です。
$$ 2^{74207281}-1$$
これは50番目のメルセンヌ素数でもあります。
（メルセンヌ素数については別途ご説明しますね）
人類歴史上の数学者は、この素数に魅せられてきました。
でも、一般人には素数の面白さはいまいちわかりません。
このページでは、エレガントで美しい素数について、少しだけご紹介したいと思います。
2357とは
2は素数。
3も素数。
5も素数。
7も素数。
2、3、5、7は、10以下の一桁の素数の全てです。
「2357」という4桁の数も、350番目の素数です。
$2+3+5+7$も素数です。
$2^{2}+3^{3}+5^{5}+7^{7}$も素数です。
$2^{19}+3^{19}+5^{19}+7^{19}$も素数です。
$2^{1013}+3^{1013}+5^{1013}+7^{1013}$も素数です。
$2\times{3}\times{5}\times{7}+2+3+5+7$も素数です。
$2\times{3}\times{5}\times{7}-2-3-5-7$も素数です。
↓こちらも、素数です。
2357223335555577777772357
最初に2357、次に2を2つ、3を3つ、5を5つ、7を7つ、最後にまた2357をくっつけた数字です。
わかりやすくするため色を変えていますが、１つの大きな桁の素数なのです。
素数2357、なんともいえない魅力のある数字だと思いませんか。
私はこの数字に魅せられて、車の希望ナンバーを素数の2357にしました。
都内でこのナンバーの車を見たら、きっとそれは私です。
1はなぜ素数ではないのか
素数の定義には、「１で割り切れる事」と、「その数自身で割り切れる」というルールがありました。
では、1自体は素数となるでしょうか。
1は1で割り切れるし、「その数自身で割り切れる」という意味で、1自身である1でも割り切れる、と考えることができるので、1も素数と考えたい方もいるかもしれません。
しかし、もし1を素数としてしまうと、2357を含むこのサイトに書いてあるほかの素数すべてが素数でなくなってしまうのです！
「素数は1だけです！」となってしまうと、他の数学的な考え方をするときに非常に不都合なため、1は素数に含めないルールになっているのです。
それはどういうことか？
二つのケースで簡単にご説明しましょう。
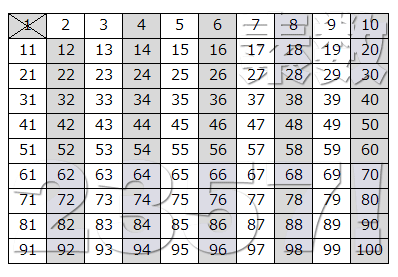
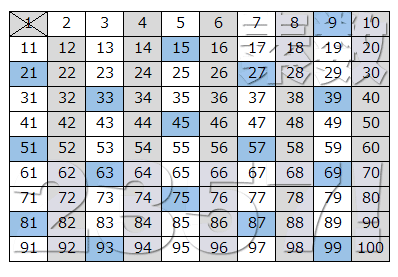
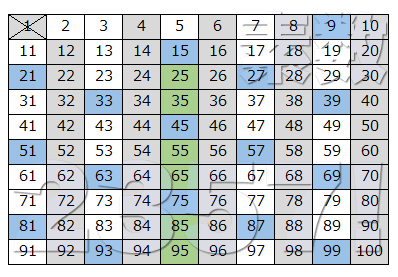
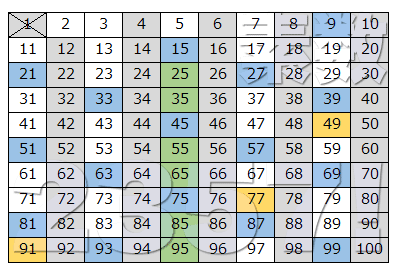
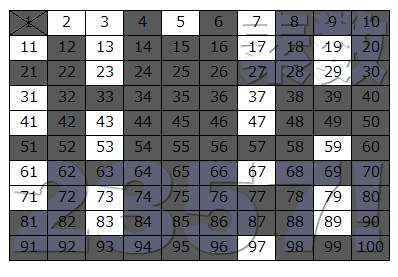
- １．エラトステネスのふるいで理解する
- ２．「素因数分解の一意性」というルールから理解する
素数の数
素数の数は、どのくらいあると思いますか？
素数の数は、無限大にあると言われています。
2018年1月現在の最大の素数は、2018年1月3日にGIMPSで発見された$2^{77232917}-1$で、2324万9425桁のメルセンヌ素数（50番目）です。
次に大きな素数は2016年1月7日に発見された49番目のメルセンヌ素数、$2^{74207281}-1$です。48番目は2013年1月に発見された$2^{57885161}-1$で、1742万5170桁のメルセンヌ素数です。
では、計算されていてわかっている素数の数がどのくらいあるのか、
1
1秭以下の素数は、184垓3559京9767兆3492億86万7866個あります。
詳細は下の表をどうぞ。
| 範囲 | 0の数 | 素数の個数 | |
|---|---|---|---|
| 10まで | 10^1 | 1 | 4 |
| 100まで | 10^2 | 2 | 25 |
| 1000まで | 10^3 | 3 | 168 |
| 1万まで | 10^4 | 4 | 1229 |
| 10万まで | 10^5 | 5 | 9592 |
| 100万まで | 10^6 | 6 | 78498 |
| 1000万まで | 10^7 | 7 | 664579 |
| 1億まで | 10^8 | 8 | 5761455 |
| 10億まで | 10^9 | 9 | 50847534 |
| 100億まで | 10^10 | 10 | 455052511 |
| 1000億まで | 10^11 | 11 | 4118054813 |
| 1兆まで | 10^12 | 12 | 37607912018 |
| 10兆まで | 10^13 | 13 | 346065536839 |
| 100兆まで | 10^14 | 14 | 3204941750802 |
| 1000兆まで | 10^15 | 15 | 29844570422669 |
| 1 | 10^16 | 16 | 279238341033925 |
| 10京まで | 10^17 | 17 | 2623557157654233 |
| 100京まで | 10^18 | 18 | 24739954287740860 |
| 1000京まで | 10^19 | 19 | 234057667276344607 |
| 1 | 10^20 | 20 | 2220819602560918840 |
| 10垓まで | 10^21 | 21 | 21127269486018731928 |
| 100垓まで | 10^22 | 22 | 201467286689315906290 |
| 1000垓まで | 10^23 | 23 | 1925320391606803968923 |
| 1 | 10^24 | 24 | 18435599767349200867866 |
素数の一覧とダウンロード
では、具体的に素数の一覧を見てみましょう。
最初の素数である2から、10000までの4桁の素数1229個全てをUPしてみました。
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991 997 1009 1013 1019 1021 1031 1033 1039 1049 1051 1061 1063 1069 1087 1091 1093 1097 1103 1109 1117 1123 1129 1151 1153 1163 1171 1181 1187 1193 1201 1213 1217 1223 1229 1231 1237 1249 1259 1277 1279 1283 1289 1291 1297 1301 1303 1307 1319 1321 1327 1361 1367 1373 1381 1399 1409 1423 1427 1429 1433 1439 1447 1451 1453 1459 1471 1481 1483 1487 1489 1493 1499 1511 1523 1531 1543 1549 1553 1559 1567 1571 1579 1583 1597 1601 1607 1609 1613 1619 1621 1627 1637 1657 1663 1667 1669 1693 1697 1699 1709 1721 1723 1733 1741 1747 1753 1759 1777 1783 1787 1789 1801 1811 1823 1831 1847 1861 1867 1871 1873 1877 1879 1889 1901 1907 1913 1931 1933 1949 1951 1973 1979 1987 1993 1997 1999 2003 2011 2017 2027 2029 2039 2053 2063 2069 2081 2083 2087 2089 2099 2111 2113 2129 2131 2137 2141 2143 2153 2161 2179 2203 2207 2213 2221 2237 2239 2243 2251 2267 2269 2273 2281 2287 2293 2297 2309 2311 2333 2339 2341 2347 2351 2357 2371 2377 2381 2383 2389 2393 2399 2411 2417 2423 2437 2441 2447 2459 2467 2473 2477 2503 2521 2531 2539 2543 2549 2551 2557 2579 2591 2593 2609 2617 2621 2633 2647 2657 2659 2663 2671 2677 2683 2687 2689 2693 2699 2707 2711 2713 2719 2729 2731 2741 2749 2753 2767 2777 2789 2791 2797 2801 2803 2819 2833 2837 2843 2851 2857 2861 2879 2887 2897 2903 2909 2917 2927 2939 2953 2957 2963 2969 2971 2999 3001 3011 3019 3023 3037 3041 3049 3061 3067 3079 3083 3089 3109 3119 3121 3137 3163 3167 3169 3181 3187 3191 3203 3209 3217 3221 3229 3251 3253 3257 3259 3271 3299 3301 3307 3313 3319 3323 3329 3331 3343 3347 3359 3361 3371 3373 3389 3391 3407 3413 3433 3449 3457 3461 3463 3467 3469 3491 3499 3511 3517 3527 3529 3533 3539 3541 3547 3557 3559 3571 3581 3583 3593 3607 3613 3617 3623 3631 3637 3643 3659 3671 3673 3677 3691 3697 3701 3709 3719 3727 3733 3739 3761 3767 3769 3779 3793 3797 3803 3821 3823 3833 3847 3851 3853 3863 3877 3881 3889 3907 3911 3917 3919 3923 3929 3931 3943 3947 3967 3989 4001 4003 4007 4013 4019 4021 4027 4049 4051 4057 4073 4079 4091 4093 4099 4111 4127 4129 4133 4139 4153 4157 4159 4177 4201 4211 4217 4219 4229 4231 4241 4243 4253 4259 4261 4271 4273 4283 4289 4297 4327 4337 4339 4349 4357 4363 4373 4391 4397 4409 4421 4423 4441 4447 4451 4457 4463 4481 4483 4493 4507 4513 4517 4519 4523 4547 4549 4561 4567 4583 4591 4597 4603 4621 4637 4639 4643 4649 4651 4657 4663 4673 4679 4691 4703 4721 4723 4729 4733 4751 4759 4783 4787 4789 4793 4799 4801 4813 4817 4831 4861 4871 4877 4889 4903 4909 4919 4931 4933 4937 4943 4951 4957 4967 4969 4973 4987 4993 4999 5003 5009 5011 5021 5023 5039 5051 5059 5077 5081 5087 5099 5101 5107 5113 5119 5147 5153 5167 5171 5179 5189 5197 5209 5227 5231 5233 5237 5261 5273 5279 5281 5297 5303 5309 5323 5333 5347 5351 5381 5387 5393 5399 5407 5413 5417 5419 5431 5437 5441 5443 5449 5471 5477 5479 5483 5501 5503 5507 5519 5521 5527 5531 5557 5563 5569 5573 5581 5591 5623 5639 5641 5647 5651 5653 5657 5659 5669 5683 5689 5693 5701 5711 5717 5737 5741 5743 5749 5779 5783 5791 5801 5807 5813 5821 5827 5839 5843 5849 5851 5857 5861 5867 5869 5879 5881 5897 5903 5923 5927 5939 5953 5981 5987 6007 6011 6029 6037 6043 6047 6053 6067 6073 6079 6089 6091 6101 6113 6121 6131 6133 6143 6151 6163 6173 6197 6199 6203 6211 6217 6221 6229 6247 6257 6263 6269 6271 6277 6287 6299 6301 6311 6317 6323 6329 6337 6343 6353 6359 6361 6367 6373 6379 6389 6397 6421 6427 6449 6451 6469 6473 6481 6491 6521 6529 6547 6551 6553 6563 6569 6571 6577 6581 6599 6607 6619 6637 6653 6659 6661 6673 6679 6689 6691 6701 6703 6709 6719 6733 6737 6761 6763 6779 6781 6791 6793 6803 6823 6827 6829 6833 6841 6857 6863 6869 6871 6883 6899 6907 6911 6917 6947 6949 6959 6961 6967 6971 6977 6983 6991 6997 7001 7013 7019 7027 7039 7043 7057 7069 7079 7103 7109 7121 7127 7129 7151 7159 7177 7187 7193 7207 7211 7213 7219 7229 7237 7243 7247 7253 7283 7297 7307 7309 7321 7331 7333 7349 7351 7369 7393 7411 7417 7433 7451 7457 7459 7477 7481 7487 7489 7499 7507 7517 7523 7529 7537 7541 7547 7549 7559 7561 7573 7577 7583 7589 7591 7603 7607 7621 7639 7643 7649 7669 7673 7681 7687 7691 7699 7703 7717 7723 7727 7741 7753 7757 7759 7789 7793 7817 7823 7829 7841 7853 7867 7873 7877 7879 7883 7901 7907 7919 7927 7933 7937 7949 7951 7963 7993 8009 8011 8017 8039 8053 8059 8069 8081 8087 8089 8093 8101 8111 8117 8123 8147 8161 8167 8171 8179 8191 8209 8219 8221 8231 8233 8237 8243 8263 8269 8273 8287 8291 8293 8297 8311 8317 8329 8353 8363 8369 8377 8387 8389 8419 8423 8429 8431 8443 8447 8461 8467 8501 8513 8521 8527 8537 8539 8543 8563 8573 8581 8597 8599 8609 8623 8627 8629 8641 8647 8663 8669 8677 8681 8689 8693 8699 8707 8713 8719 8731 8737 8741 8747 8753 8761 8779 8783 8803 8807 8819 8821 8831 8837 8839 8849 8861 8863 8867 8887 8893 8923 8929 8933 8941 8951 8963 8969 8971 8999 9001 9007 9011 9013 9029 9041 9043 9049 9059 9067 9091 9103 9109 9127 9133 9137 9151 9157 9161 9173 9181 9187 9199 9203 9209 9221 9227 9239 9241 9257 9277 9281 9283 9293 9311 9319 9323 9337 9341 9343 9349 9371 9377 9391 9397 9403 9413 9419 9421 9431 9433 9437 9439 9461 9463 9467 9473 9479 9491 9497 9511 9521 9533 9539 9547 9551 9587 9601 9613 9619 9623 9629 9631 9643 9649 9661 9677 9679 9689 9697 9719 9721 9733 9739 9743 9749 9767 9769 9781 9787 9791 9803 9811 9817 9829 9833 9839 9851 9857 9859 9871 9883 9887 9901 9907 9923 9929 9931 9941 9949 9967 9973
すごいですね、美しいですね。
こうした素数の一覧は、下のリストからダウンロード可能ですので、ご興味のある方は自由にダウンロードしてくださいね。
- ダウンロードリストを表示
メルセンヌ素数とは？
素数の中で、メルセンヌ数の素数を「メルセンヌ素数」と呼びます。
このページでは、メルセンヌ数とメルセンヌ素数の説明に加えて、メルセンヌ素数の一覧をダウンロードできるようにしてあります。
メルセンヌ数って何？
メルセンヌ数の求め方は、1、2、3、4、…という自然数を$n$とした時に、$2^{n}-1$の式で求めることができます。この答えがメルセンヌ数です。
このメルセンヌ数が素数の時、その素数を「メルセンヌ素数」と呼びます。
答えが素数の時は$n$も素数です。（しかし$n$が素数でも、答えは全てが素数にはなりません。）
メルセンヌ素数は $2^{p}-1=M_p$という数式で表すこともあります。
メルセンヌ数はとても面白い特徴を持った数字です。もう少し詳しくメルセンヌ数を理解してみましょう。
メルセンヌ数を計算してみよう
まず、$2^{n}-1$の$n$に数字を当てはめて計算してみましょう。
※例: $2^{3}=2\times{2}\times{2}$です。
$n=2$の場合 $2^{2}-1=3$
$n=3$の場合 $2^{3}-1=7$
$n=4$の場合 $2^{4}-1=15$
$n=5$の場合 $2^{5}-1=31$
$n=6$の場合 $2^{6}-1=63$
$n=7$の場合 $2^{7}-1=127$
$n=8$の場合 $2^{8}-1=255$
$n=9$の場合 $2^{9}-1=511$
上の赤い行は素数ですからメルセンヌ素数です。
メルセンヌ数の何が面白いかというと、これらの数値を2進数にしたときに全部1になるのです。
「？？」ですか？
二進数って何？
2進数とは、0と1だけで表す数のことで、2で桁が上がる数字です。
でも私たちは10で桁が上がる10進数を使いますから馴染みがありませんね。数字を2進数になおして理解してみましょう。
| 10進数 | 2進数 | 2進数にする考え方 |
|---|---|---|
| 0 | 0 | 0と1は10進数も2進数も同じ |
| 1 | 1 | |
| 2 | 10 | 1と0しか使えないので、2は桁を増やして「10」 |
| 3 | 11 | 3は2の「10」の1桁目を1にして「11」 |
| 4 | 100 | 1と0しか使えないので、4は桁を増やして「100」 |
| 5 | 101 | 5は4の「100」の1桁目を1にして「101」 |
| 6 | 110 | 6は5の「101」の2桁目を1にし、1桁目を0にして「110」 |
| 7 | 111 | 7は6の「110」の1桁目を1にして「111」 |
| 8 | 1000 | 1と0しか使えないので、8は桁を増やして「1000」 |
| 9 | 1001 | |
| 10 | 1010 | |
| 11 | 1011 | |
| 12 | 1100 | |
| 13 | 1101 | |
| 14 | 1110 | |
| 15 | 1111 |
↑この一覧表で赤文字の部分を見て下さい。
2進数にしたときに、全部1の数字がありますね。これがメルセンヌ数なのです。上の表ですと、3、7、15です。更にメルセンヌ数は、31、63、127、255、511、1023、2047、8191と続きます。
では、$2^{n}-1$で計算した答えを二進数になおしてみましょう。赤字はメルセンヌ素数です。
$2^{2}-1=3$ 二進数では$11$
$2^{3}-1=7$ 二進数では$111$
$2^{4}-1=15$ 二進数では$1111$
$2^{5}-1=31$ 二進数では$11111$
$2^{6}-1=63$ 二進数では$111111$
$2^{7}-1=127$ 二進数では$1111111$
$2^{8}-1=255$ 二進数では$11111111$
$2^{9}-1=511$ 二進数では$111111111$
※よく見ると、メルセンヌ数を2進数に直すと$n$の数に等しい回数だけ、1が並ぶことがわかりますね。
このうなメルセンヌ数の特徴から、メルセンヌ素数も2進数にすると1が$n$回並ぶ素数なのです。面白いですね！（面白くないか。）
メルセンヌ素数一覧・ダウンロード
現在までに分かっている50個のメルセンヌ素数の$2^{p}-1=M_p$の式を一覧にしました。
途中までメルセンヌ素数（計算結果）も併記しました。（素数自体が大きいものは、クリックすると答えが表示され、もう一度クリックすると答えが隠れます。）
2018年1月現在最大の50番目の素数は$2^{77232917}-1$です。$2^{77232917}-1$とは、${2}\times{2}\times{2}$…と、$77232917$回掛け算してから1を引いた数です。2324万9425桁の数字なんですよ！この素数だけが書いてあるデータでも24MBになってしまうほどの量なんです！すごいですね～！
49番目のメルセンヌ素数では$2^{74207281}-1$で、2233万8618桁もありますし、48番目のメルセンヌ素数$2^{57885161}-1=$も1742万5170桁あり、48番目の素数を書いたファイルでさえ17メガバイト(MB)を超えるサイズになります！
※$2^{11213}-1$以降どんどん桁数が大きくなるので、式のみ記載しました。これらのメルセンヌ素数が必要な方は、下部からメルセンヌ素数一覧をダウンロードできます。
- $2^{2}-1=3$
- $2^{3}-1=7$
- $2^{5}-1=31$
- $2^{7}-1=127$
- $2^{13}-1=8191$
- $2^{17}-1=131071$
- $2^{19}-1=524287$
- $2^{31}-1=2147483647$
- $2^{61}-1=2305843009213693951$
- $2^{89}-1=$素数を表示
- 618970019642690137449562111
- $2^{107}-1=$素数を表示
- 162259276829213363391578010288127
- $2^{127}-1=$素数を表示
- 170141183460469231731687303715884105727
- $2^{521}-1=$素数を表示
- 6864797660130609714981900799081393217269435300143305409394463459185543183397656052122559640661454554977296311391480858037121987999716643812574028291115057151
- $2^{607}-1=$素数を表示
- 531137992816767098689588206552468627329593117727031923199444138200403559860852242739162502265229285668889329486246501015346579337652707239409519978766587351943831270835393219031728127
- $2^{1279}-1=$素数を表示
- 10407932194664399081925240327364085538615262247266704805319112350403608059673360298012239441732324184842421613954281007791383566248323464908139906605677320762924129509389220345773183349661583550472959420547689811211693677147548478866962501384438260291732348885311160828538416585028255604666224831890918801847068222203140521026698435488732958028878050869736186900714720710555703168729087
- $2^{2203}-1=$素数を表示
- 1475979915214180235084898622737381736312066145333169775147771216478570297878078949377407337049389289382748507531496480477281264838760259191814463365330269540496961201113430156902396093989090226259326935025281409614983499388222831448598601834318536230923772641390209490231836446899608210795482963763094236630945410832793769905399982457186322944729636418890623372171723742105636440368218459649632948538696905872650486914434637457507280441823676813517852099348660847172579408422316678097670224011990280170474894487426924742108823536808485072502240519452587542875349976558572670229633962575212637477897785501552646522609988869914013540483809865681250419497686697771007
- $2^{2281}-1=$素数を表示
- 446087557183758429571151706402101809886208632412859901111991219963404685792820473369112545269003989026153245931124316702395758705693679364790903497461147071065254193353938124978226307947312410798874869040070279328428810311754844108094878252494866760969586998128982645877596028979171536962503068429617331702184750324583009171832104916050157628886606372145501702225925125224076829605427173573964812995250569412480720738476855293681666712844831190877620606786663862190240118570736831901886479225810414714078935386562497968178729127629594924411960961386713946279899275006954917139758796061223803393537381034666494402951052059047968693255388647930440925104186817009640171764133172418132836351
- $2^{3217}-1=$素数を表示
- 259117086013202627776246767922441530941818887553125427303974923161874019266586362086201209516800483406550695241733194177441689509238807017410377709597512042313066624082916353517952311186154862265604547691127595848775610568757931191017711408826252153849035830401185072116424747461823031471398340229288074545677907941037288235820705892351068433882986888616658650280927692080339605869308790500409503709875902119018371991620994002568935113136548829739112656797303241986517250116412703509705427773477972349821676443446668383119322540099648994051790241624056519054483690809616061625743042361721863339415852426431208737266591962061753535748892894599629195183082621860853400937932839420261866586142503251450773096274235376822938649407127700846077124211823080804139298087057504713825264571448379371125032081826126566649084251699453951887789613650248405739378594599444335231188280123660406262468609212150349937584782292237144339628858485938215738821232393687046160677362909315071
- $2^{4253}-1=$素数を表示
- 190797007524439073807468042969529173669356994749940177394741882673528979787005053706368049835514900244303495954950709725762186311224148828811920216904542206960744666169364221195289538436845390250168663932838805192055137154390912666527533007309292687539092257043362517857366624699975402375462954490293259233303137330643531556539739921926201438606439020075174723029056838272505051571967594608350063404495977660656269020823960825567012344189908927956646011998057988548630107637380993519826582389781888135705408653045219655801758081251164080554609057468028203308718724654081055323215860189611391296030471108443146745671967766308925858547271507311563765171008318248647110097614890313562856541784154881743146033909602737947385055355960331855614540900081456378659068370317267696980001187750995491090350108417050917991562167972281070161305972518044872048331306383715094854938415738549894606070722584737978176686422134354526989443028353644037187375385397838259511833166416134323695660367676897722287918773420968982326089026150031515424165462111337527431154890666327374921446276833564519776797633875503548665093914556482031482248883127023777039667707976559857333357013727342079099064400455741830654320379350833236245819348824064783585692924881021978332974949906122664421376034687815350484991
- $2^{4423}-1=$素数を表示
- 285542542228279613901563566102164008326164238644702889199247456602284400390600653875954571505539843239754513915896150297878399377056071435169747221107988791198200988477531339214282772016059009904586686254989084815735422480409022344297588352526004383890632616124076317387416881148592486188361873904175783145696016919574390765598280188599035578448591077683677175520434074287726578006266759615970759521327828555662781678385691581844436444812511562428136742490459363212810180276096088111401003377570363545725120924073646921576797146199387619296560302680261790118132925012323046444438622308877924609373773012481681672424493674474488537770155783006880852648161513067144814790288366664062257274665275787127374649231096375001170901890786263324619578795731425693805073056119677580338084333381987500902968831935913095269821311141322393356490178488728982288156282600813831296143663845945431144043753821542871277745606447858564159213328443580206422714694913091762716447041689678070096773590429808909616750452927258000843500344831628297089902728649981994387647234574276263729694848304750917174186181130688518792748622612293341368928056634384466646326572476167275660839105650528975713899320211121495795311427946254553305387067821067601768750977866100460014602138408448021225053689054793742003095722096732954750721718115531871310231057902608580607
- $2^{9689}-1=$素数を表示
- 4782202788054612029528392986600059097414971724022365008513345109918378950942662970278927686112707894586824720981524256319306585052676834087480834429433264797425893247623688331021633208954847354805799943341309825989013743806187109581043148680813778321530496715601563282624414040398143207622036272190408590790537203475256105564071579263867875240985573356522656108542128577321057879052328865035355873615679363655889925711574420153832091752422843046918811427400662135559303516853703976812686385750376227787949580582081831261725701003498206512329872677233489510953469375683037038373999696771585788905639115522613405495707184524158219208223766442059014593330657009722153962376853423770486138578089775621301167811299166407361746606697808186757966914671246073712904200588408923186387737887675292886953797066980967406053530122853539036965490224784924649007954898678503314655546475504501686187354866964374552614120640782949622452027788962138602665933147687696322089504278791624651519312327831756553779377194524673395819281486668576384019590720179413349582970319393884388810494546040342087536563628332152073181614300721769371426238517540520845214665313301183551962591849558938499025348780376716477073930634436840084468255937443451690315999349137664638968972614199015304906547819056227171224947070739716300953775743441307920501863532234466545645695774331885044978250148663467372130392099894852145190998232878772486650513010816769902892518719250066947215706536216248696240569256865554296221552211560427778662545936998801070186162601476474293459830183651273363462732675883060701410359254829149774339297173680765610959599911309189788238350131635672661435969218239977196933874395403996623675580528211207136396370858056051160781770985452576988032333812939272752101944629527490313835551985197095928885236415301789218675141014541203096191270934369039522098280317668942061325572349643638403056487349290884223786292887472231219032385281034091824306618947740727265524284893304474861454942076799041739447165838281671410435831206790501914527326287370339974707206016882562827404270170322606727980343479326425730091839813077719322455394763960606588214326603156141490740557698055166263044447583756711516490181193442236859424151843795389335765432129944054855345155859273424561825146813714720606287781021240923708021492298349635179527270302962970156927686511635050080407282674252362644695710769768866137302789313609674382719017385508484663373476120843567983065059558072935110637544240807350667082987233779768874938983584523095638996120616318634391967112086464384649470963230072729200912586147267999762496709852769503535733924416202657720741248683592202828983311140833923302433917797976990311425843619350936754483811194408812763388084204451804912454383884180800945275626668057628954763384641305107753773247082495804533355717481965025070819730466422826105697510564289798951182192885976352229053898948737614642139910911535864505818992696826225754111
- $2^{9941}-1=$素数を表示
- 34608828249085121524296039576741331672262866890023854779048928344500622080983411446436437554415370753366448674763505018641470709332373970608376690404229265789647993709760358469552319045484910050304149809818540283507159683562232941968059762281334544739720849260904855192770626054911793590389060795981163838721432994278763633095377438194844866471124967685798888172212033000821469684464956146997194126921284336206463313859537577200462442029064681326087558257488470489384243989270236884978643063093004422939603370010546595386302009073043944482202559097406700597330570799507832963130938739885080198416258635194522913042562936679859587495721031173747796418895060701941717506001937152430032363631934265798516236047451209089864707430780362298307038193445486493756647991804258775574973833903315735082891029392359352758617185019942554834671861074548772439880729606244911940066680112823824095816458261761861746604034802056466823143718255492784779380991749580255263323326536457743894150848953969902818530057870876229329803338285735419228259022169602665532210834789602051686546011466737981306056247480055071718250333737502267307344178512950738594330684340802698228963986562732597175372087295649072830289749771358330867951508710859216743218522918811670637448496498549094430541277444079407989539857469452772132166580885754360477408842913327292948696897496141614919739845432835894324473601387609643750514699215032683744527071718684091832170948369396280061184593746143589068811190253101873595319156107319196071150598488070027088705842749605203063194191166922106176157609367241948160625989032127984748081075324382632093913796444665700601391278360323002267434295194325607280661260119378719405151497555187549252134264394645963853964913309697776533329401822158003182889278072368602128982710306618115118964131893657845400296860012420391376964670183983594954112484565597312460737798777092071706710824503707457220155015899591766244957768006802482976673920392995410164224776445671222149803657927708412925555542817045572430846389988129960519227313987291200902060882060733762075892299473666405897427035811786879875694315078654420055603469625309399653955932310466430039146465805452965014040019423897552675534768248624631951431493188170905972588780111850281190559073677771187432814088678674286302108275149258477101296451833651979717375170900505673645964696355331369819296000267389583289299126738345726980325998955997501176664201042888546085699446442834195232948787488410595750197438786353119204210855804692460582533832967771946911459901921324984968810021189968284941331573164056304725480868921823442538199590383852412786840833479611419970101792978355653650755329138298654246225346827207503606740745956958127383748717825918527473164970582095181312905519242710280573023145554793628499010509296055849712377978984921839997037415897674154830708629145484724536724572622450131479992681684310464449439022250504859250834761894788889552527898400988196200014868575640233136509145628127191354858275083907891469979019426224883789463551
- $2^{11213}-1$ ※
- $2^{19937}-1$
- $2^{21701}-1$
- $2^{23209}-1$
- $2^{44497}-1$
- $2^{86243}-1$
- $2^{110503}-1$
- $2^{132049}-1$
- $2^{216091}-1$
- $2^{756839}-1$
- $2^{859433}-1$
- $2^{1257787}-1$
- $2^{1398269}-1$
- $2^{2976221}-1$
- $2^{3021377}-1$
- $2^{6972593}-1$
- $2^{13466917}-1$
- $2^{20996011}-1$
- $2^{24036583}-1$
- $2^{25964951}-1$
- $2^{30402457}-1$
- $2^{32582657}-1$
- $2^{37156667}-1$
- $2^{42643801}-1$
- $2^{43112609}-1$
- $2^{57885161}-1$
- $2^{74207281}-1$
- $2^{77232917}-1$
- 一覧ダウンロード
- メルセンヌ素数式一覧ダウンロードはこちらからどうぞ。(Mersenne_prime.txt 1.1MB)
単なる素数も美しいですが、メルセンヌ素数はさらにエレガントな魅力がありますね！
50番目のメルセンヌ素数$2^{77232917}-1$は、2324万9425桁の素数ですが、パソコン（0と1で考える2進数）でこのメルセンヌ素数$2^{77232917}-1$を表示するときには、7723万2917個の1が並んだ2進数になります。
2進数って面白いでしょ？（面白って言って！笑）
素数の謎
素数は、どのような規則で現れるかまだわかっていません。
オイラーという数学者が、$2,\ 3,\ 5,\ 7,\ 11,\ 13$...と続く素数を、下のように計算しました。
$ \frac{2^{2}}{2^{2}-1}\times\frac{3^{2}}{3^{2}-1}\times\frac{5^{2}}{5^{2}-1}\times\frac{7^{2}}{7^{2}-1}\times\frac{11^{2}}{11^{2}-1} $...
するとその答えは、 $$\displaystyle{=\frac{\pi^{2}}{6}}$$ と、円周率に関係がある結果になりました。無秩序に現れる素数には、やはり何か規則があるのかも知れないとわかったのです。
素数を使ったオイラーの計算式を参考に、数学者リーマンが下の「ゼータ関数」を考えます。
$\displaystyle{ \zeta\left({s}\right)= \sum_{{n}=1}^{\infty}\frac{1}{{n}^{-1}} =\prod_{{p:prime}}\Biggl(1-\frac{1}{p^{s}}\Biggr)^{-1} }$
リーマンは素数をゼータ関数で計算しグラフにすると、零点が一直線上に並ぶことを発見しました。（このゼータ関数の零点分布の解説で本1冊分ほどの情報量です！）
この事から、「複素の零点はすべて実部が$\displaystyle{\frac{1}{2}}$である」（$=$すべての零点は一直線上にあるはず）と仮説を立てました。これが有名な「リーマン予想」です。
リーマン予想は数学上の大難問で、未だにこの仮説を証明・否定できた人はいません。もし解決できた場合、クレイ数学研究所というところから100万ドルの懸賞金がもらえます。（日本円で1億円くらい）
また、素数のゼータ関数の零点分布を現す数式は、原子核エネルギー間隔の数式と完全に一致していることもわかり、物理の分野にも深い関係がありそうです。
不思議で魅力的な素数・・・。
これから先、どんな研究がされどんな答えが導かれるのでしょうね。
この「素数2357」を見て素数に興味を持ち、将来リーマン予想を証明し1億円稼ぐ天才が現れたら楽しいなと思いつつ、当サイトは製作されました。ご意見・ご感想などお寄せ頂ければ嬉しいです。
数の単位
このサイトはとにかく素数だけのサイトなのですが、素数の数が大きくなると数の単位も大きくなります。
万、億、兆、京、
- 数の単位一覧を表示
-
$10^{0}$ 一
$10^{1}$ 十
$10^{2}$ 百
$10^{3}$ 千
$10^{4}$ 万
$10^{8}$ 億
$10^{12}$ 兆
$10^{16}$ 京 （けい）
$10^{20}$ 垓 （がい）
$10^{24}$ 秭 （じょ）
$10^{28}$ 穰 （じょう）
$10^{32}$ 溝 （こう）
$10^{36}$ 澗 （かん）
$10^{40}$ 正 （せい）
$10^{44}$ 載 （さい）
$10^{48}$ 極 （ごく）
$10^{52}$ 恒河沙 （ごうがしゃ）
$10^{56}$ 阿僧祇 （あそうぎ）
$10^{60}$ 那由他 （なゆた）
$10^{64}$ 不可思議 （ふかしぎ）
$10^{68}$ 無量大数 （むりょうたいすう）
[仏典の数詞 華厳経命数]
$10^{7}$ 倶胝 （くてい）
$10^{14}$ 阿ゆ多 （あゆた）
$10^{28}$ 那由他 （なゆた）
$10^{56}$ 頻波羅 （びんばら）
$10^{112}$ 矜羯羅 （こんがら）
$10^{224}$ 阿伽羅 （あから）
$10^{448}$ 最勝 （さいしょう）
$10^{896}$ 摩婆羅 （まばら）
$10^{1792}$ 阿婆羅 （あばら）
$10^{3584}$ 多婆羅 （たばら）
$10^{7168}$ 界分 （かいぶん）
$10^{14336}$ 普摩 （ふま）
$10^{28672}$ 禰摩 （ねま）
$10^{57344}$ 阿婆詹 （あばけん）
$10^{114688}$ 弥伽婆 （みかば）
$10^{229376}$ 毘ら伽 （びらか）
$10^{458752}$ 毘伽婆 （びかば）
$10^{917504}$ 僧羯邏摩 （そうがらま）
$10^{1835008}$ 毘薩羅 （びさら）
$10^{3670016}$ 毘贍婆 （びせんば）
$10^{7340032}$ 毘盛伽 （びじょうが）
$10^{14680064}$ 毘素陀 （びすだ）
$10^{29360128}$ 毘婆訶 （びばか）
$10^{58720256}$ 毘薄底 （びばてい）
$10^{117440512}$ 毘きゃ擔 （びきゃたん）
$10^{234881024}$ 称量 （しょうりょう）
$10^{469762048}$ 一持 （いちじ）
$10^{939524096}$ 異路 （いろ）
$10^{1879048192}$ 顛倒 （てんどう）
$10^{3758096384}$ 三末耶 （さんまや）
$10^{7516192768}$ 毘睹羅 （びとら）
$10^{15032385536}$ 奚婆羅 （けいばら）
$10^{30064771072}$ 伺察 （しさつ）
$10^{60129542144}$ 周広 （しゅうこう）
$10^{120259084288}$ 高出 （こうしゅつ）
$10^{240518168576}$ 最妙 （さいみょう）
$10^{481036337152}$ 泥羅婆 （ないらば）
$10^{962072674304}$ 訶理婆 （かりば）
$10^{1924145348608}$ 一動 （いちどう）
$10^{3848290697216}$ 訶理蒲 （かりぼ）
$10^{7696581394432}$ 訶理三 （かりさん）
$10^{15393162788864}$ 奚魯伽 （けいろか）
$10^{30786325577728}$ 達ら歩陀 （たつらほだ）
$10^{61572651155456}$ 訶魯那 （かろな）
$10^{123145302310912}$ 摩魯陀 （まろだ）
$10^{246290604621824}$ 懺慕陀 （ざんぼだ）
$10^{492581209243648}$ えらい陀 （えいらだ）
$10^{985162418487296}$ 摩魯摩 （まろま）
$10^{1970324836974592}$ 調伏 （ちょうぶく）
$10^{3940649673949184}$ 離きょう慢 （りきょうまん）
$10^{7881299347898368}$ 不動 （ふどう）
$10^{15762598695796736}$ 極量 （ごくりょう）
$10^{31525197391593472}$ 阿麼怛羅 （あまたら）
$10^{63050394783186944}$ 勃麼怛羅 （ぼまたら）
$10^{126100789566373888}$ 伽麼怛羅 （がまたら）
$10^{252201579132747776}$ 那麼怛羅 （なまたら）
$10^{504403158265495552}$ 奚麼怛羅 （けいまたら）
$10^{1008806316530991104}$ べい麼怛羅 （べいまたら）
$10^{2017612633061982208}$ 鉢羅麼怛羅 （はらまたら）
$10^{4035225266123964416}$ 尸婆麼怛羅 （しばまたら）
$10^{8070450532247928832}$ 翳羅 （えいら）
$10^{16140901064495857664}$ 薜羅 （べいら）
$10^{32281802128991715328}$ 諦羅 （たいら）
$10^{64563604257983430656}$ 偈羅 （げら）
$10^{129127208515966861312}$ そ歩羅 （そほら）
$10^{258254417031933722624}$ 泥羅 （ないら）
$10^{516508834063867445248}$ 計羅 （けいら）
$10^{1033017668127734890496}$ 細羅 （さいら）
$10^{2066035336255469780992}$ 睥羅 （へいら）
$10^{4132070672510939561984}$ 謎羅 （めいら）
$10^{8264141345021879123968}$ 娑ら荼 （しゃらだ）
$10^{16528282690043758247936}$ 謎魯陀 （めいろだ）
$10^{33056565380087516495872}$ 契魯陀 （けいろだ）
$10^{66113130760175032991744}$ 摩睹羅 （まとら）
$10^{132226261520350065983488}$ 娑母羅 （しゃもら）
$10^{264452523040700131966976}$ 阿野娑 （あやしゃ）
$10^{528905046081400263933952}$ 迦麼羅 （かまら）
$10^{1057810092162800527867904}$ 摩伽婆 （まかば）
$10^{2115620184325601055735808}$ 阿怛羅 （あたら）
$10^{4231240368651202111471616}$ 醯魯耶 （けいろや）
$10^{8462480737302404222943232}$ 薜魯婆 （べいろば）
$10^{16924961474604808445886464}$ 羯羅波 （からは）
$10^{33849922949209616891772928}$ 訶婆婆 （かばば）
$10^{67699845898419233783545856}$ 毘婆羅 （びばら）
$10^{135399691796838467567091712}$ 那婆羅 （なばら）
$10^{270799383593676935134183424}$ 摩ら羅 （まらら）
$10^{541598767187353870268366848}$ 娑婆羅 （しゃばら）
$10^{1083197534374707740536733696}$ 迷ら普 （めいらふ）
$10^{2166395068749415481073467392}$ 者麼羅 （しゃまら）
$10^{4332790137498830962146934784}$ 駄麼羅 （だまら）
$10^{8665580274997661924293869568}$ 鉢ら麼陀 （はらまだ）
$10^{17331160549995323848587739136}$ 毘迦摩 （びかま）
$10^{34662321099990647697175478272}$ 烏波跋多 （うはばた）
$10^{69324642199981295394350956544}$ 演説 （えんぜつ）
$10^{138649284399962590788701913088}$ 無尽 （むじん）
$10^{277298568799925181577403826176}$ 出生 （しゅっしょう）
$10^{554597137599850363154807652352}$ 無我 （むが）
$10^{1109194275199700726309615304704}$ 阿畔多 （あばんた）
$10^{2218388550399401452619230609408}$ 青蓮華 （しょうれんげ）
$10^{4436777100798802905238461218816}$ 鉢頭摩 （はどま）
$10^{8873554201597605810476922437632}$ 僧祇 （そうぎ）
$10^{17747108403195211620953844875264}$ 趣 （しゅ）
$10^{35494216806390423241907689750528}$ 至 （し）
$10^{70988433612780846483815379501056}$ 阿僧祇 （あそうぎ）
$10^{141976867225561692967630759002112}$ 阿僧祇転 （あそうぎてん）
$10^{283953734451123385935261518004224}$ 無量 （むりょう）
$10^{567907468902246771870523036008448}$ 無量転 （むりょうてん）
$10^{1135814937804493543741046072016896}$ 無辺 （むへん）
$10^{2271629875608987087482092144033792}$ 無辺転 （むへんてん）
$10^{4543259751217974174964184288067584}$ 無等 （むとう）
$10^{9086519502435948349928368576135168}$ 無等転 （むとうてん）
$10^{18173039004871896699856737152270336}$ 不可数 （ふかすう）
$10^{36346078009743793399713474304540672}$ 不可数転 （ふかすうてん）
$10^{72692156019487586799426948609081344}$ 不可称 （ふかしょう）
$10^{145384312038975173598853897218162688}$ 不可称転 （ふかしょうてん）
$10^{290768624077950347197707794436325376}$ 不可思 （ふかし）
$10^{581537248155900694395415588872650752}$ 不可思転 （ふかしてん）
$10^{1163074496311801388790831177745301504}$ 不可量 （ふかりょう）
$10^{2326148992623602777581662355490603008}$ 不可量転 （ふかりょうてん）
$10^{4652297985247205555163324710981206016}$ 不可説 （ふかせつ）
$10^{9304595970494411110326649421962412032}$ 不可説転 （ふかせつてん）
$10^{18609191940988822220653298843924824064}$ 不可説不可説 （ふかせつふかせつ）
$10^{37218383881977644441306597687849648128}$ 不可説不可説転 （ふかせつふかせつてん）
日本で言われる大きな数「不可説不可説転」とは10の37澗乗で、$10^{7\times{2}^{122}}$です。
不可説不可説転のゼロの数は37218383881977644441306597687849648128個。
37澗
2183溝
8388穣
1977秭
6444垓
4130京
6597兆
6878億
4964万
8128個と読みます。
海外で大きい数字はグーグルプレックス(one googolplex) $10^{10^{10^{100}}}$や、スキューズ数(Skewes number)$10^{10^{10^{963}}}$などが挙げられています。
いずれにせよ最大はグラハム数(Graham's number) ということになっているようです。
リンク
素数に関連するWikiリンクや、その他のリンクを掲載します。
- リンクを表示
私の好きな本の一節
「よく人から数学をやって何になるのかと聞かれるが、私は春の野に咲くスミレはただスミレらしく咲いているだけでいいと思っている。咲くことがどんなによいことであろうとなかろうと、それはスミレのあずかり知らないことだ。咲いているのといないのではおのずから違うというだけのことである。私についていえば、ただ数学を学ぶ喜びを食べて生きているというだけである。そしてその喜びは『発見の喜び』にほかならない」
岡潔著「春宵十話」より
