1はなぜ素数ではないのか
素数の定義には、「1で割り切れる事」と、「その数自身で割り切れる」というルールがありました。
では、1自体は素数となるでしょうか。
1は1で割り切れるし、「その数自身で割り切れる」という意味で、1自身である1でも割り切れる、と考えることができるので、1も素数と考えたい方もいるかもしれません。
しかし、もし1を素数としてしまうと、2357を含むこのサイトに書いてあるほかの素数すべてが素数でなくなってしまうのです!
「素数は1だけです!」となってしまうと、他の数学的な考え方をするときに非常に不都合なため、1は素数に含めないルールになっているのです。
それはどういうことか?
二つのケースで簡単にご説明しましょう。
1.エラトステネスのふるいで理解する
たとえば、1, 2, 3, 4,…と数字を100まで表に書いて、そこから素数を見つけることにしましょう。
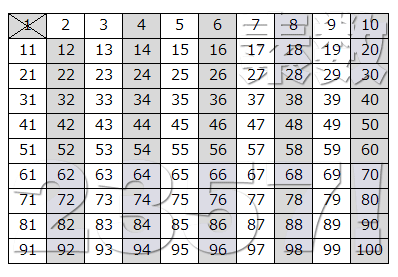
↑まず2が素数であるとわかった場合、単純にその数字の表から2の倍数である4, 6, 8, 10...を消します。残った数が素数である可能性がある、ということになりますね。
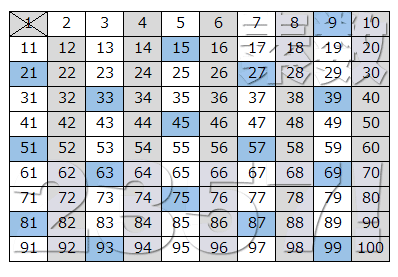
↑さらに3も素数ですので、3の倍数を消していきます。4はすでに2の倍数として消されていますので、次は5を検証することになります。
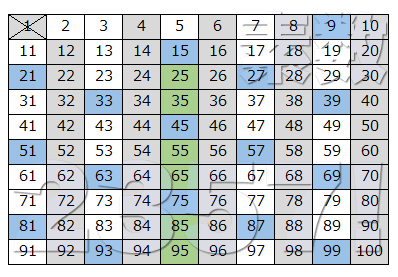
↑残った表から5の倍数を消していきます。
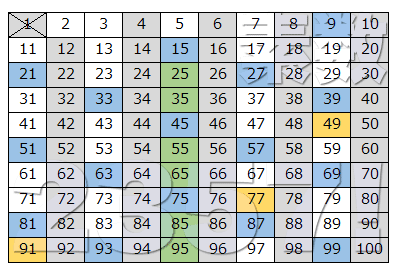
↑残った表から7の倍数を消していきます。
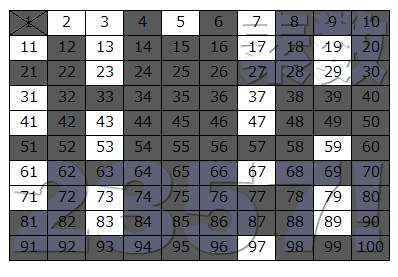
↑表からまだ消されていない数を見てみましょう。
「2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97」と、100以下の素数が残りましたね。
このような作業をすることによって、当初は1~100までの表の数字があったものが、どんどん少なくなっていき、素早く素数を見つけることができるようになります。
このアルゴリズム(計算方法)を「エラトステネスのふるい」と呼びます。
ではこのエラトステネスのふるいの作業のときに、1を素数として考えてしまったらどうなるでしょうか。
「全ての整数は1と-1の倍数であり、=1は全ての自然数の約数」という数学的な性質から、1を素数としてしまった場合、1, 2, 3, 4, 5…全てが1の倍数となり、1を素数としてしまった瞬間に、表に書いた全ての数が消えてしまうのです。
すなわち、「1を素数としてしまうと、素数は1以外にない」ということになってしまうため、1は素数から外しています。
2.「素因数分解の一意性」というルールから理解する
たとえば6の因数は1, 2, 3です。素因数とは、これらの中で素数の2と3だけが該当します。(2x3=6)
では、ここで1を素数として考えてしまった場合はどうでしょうか。1は、何度1をかけてもかけても数字が変わりません。
ですから仮に1を素数としてしまった場合、6の素因数分解は、1x2x3=6だし、1x1x1x1x2x3=6でもあるし...、ときりがなくなってしまうため、1を素数として考えないようになっています。
以上、考え方は色々ありますが、「1がなぜ素数ではないのか」、少しだけお分かりいただけたでしょうか。
素数2357も素敵ですが、1や0という数字もとても奥が深くて魅力的ですよね。1や0に関しては、また機会があったらサイトを制作したいと考えています。
 素数2357
素数2357
